Wicho´s Blog
Optimización I 2019
Acerca de mí

Hola...
Mi nombre es Luis Angel Espinoza Santiago tengo 20 años, cumplo 21 el próximo 21 de septiembre; me gusta leer, ir al cine, ver series e ir de fiesta, escuchar música de cualquier tipo con una excepción pues detesto la banda,cocinar, nadar, bailar, la danza y pertenecía al Ballet Folklorico del Valle de México A. C.
Este blog es para desarrollar actividades y tareas para la materia de Optimización I en la carrera de Matemáticas Aplicadas y Computación.
Mi nombre es Luis Angel Espinoza Santiago tengo 20 años, cumplo 21 el próximo 21 de septiembre; me gusta leer, ir al cine, ver series e ir de fiesta, escuchar música de cualquier tipo con una excepción pues detesto la banda,cocinar, nadar, bailar, la danza y pertenecía al Ballet Folklorico del Valle de México A. C.
Este blog es para desarrollar actividades y tareas para la materia de Optimización I en la carrera de Matemáticas Aplicadas y Computación.
Tarea 3 Arana Rayón Lesly & Espinoza Santiago Luis Angel
| CONCEPTO | CARACTERÍSTICA |
|
|
|
|
|
|
| Utilizada en el método simplex, donde se agregan variables de holgura o exceso para eliminar las restricciones y convertir estas en igualdad |
| En toda Ax b se puede agregar una variable en la restricción para convertirse en igualdad sumando una variable de holgura con elementos |
| En toda Ax b se puede agregar una variable en la restricción para convertirse en igualdad restando una variable de exceso con elementos |
| Son aquellas variables que valen ≠ 0 pues resuelven el sistema |
| Son aquellas variables que valen 0 |
| Es una variable no básica que en el siguiente punto extremo adyacente se convierte en básica |
| Es una variable básica que en el siguiente punto extremo adyacente se convierte en no básica |
|
|
|
|
| Forma estándar Variables deben ser no negativas Solo incluye variables de holgura Los 0 Trabaja en la región factible |
| En Max una solución básica factibles es óptima si En Min una solución básica factibles es óptima si |
| Cuando en un problema la solución básica factible inicial no pertenece a la región factible Pe puede agregar una variable artificial donde el origen si pertenece para empezar a trabajar ahí y posteriormente regresar a la forma estándar. |
| A las restricciones de la forma estandar se les agrega una variable artificial cuando estas sean El origen pertenece a la región factible |
| De penalización o Charnes Para construir a partir de la solución inicial del modelo ampliado y dar una solución básica factible del modelo original con la ayuda de las variables artificiales. Por lo que se deben aumentar las variables artificiales con coeficiente negativo (maximización ) o coeficiente positivo(minimización) denotados por M o –M que es la penalización |
| Para construir a partir de la solución inicial del modelo ampliado y dar una solución básica factible del modelo original con la ayuda de las variables artificiales. Se basa en dos fases: Fase 1: trabaja fuera de la región factible y convierte a las variables artificiales en 0 Fase 2: Elimina las variables artificiales y encuentra la solución factible |
| No utiliza el exceso de información que el método simplex utiliza Utiliza matrices y vectores para resolver el método Dónde: ( Recursos b= A= X= |
| Matriz base B Es una matriz cuadrada de m x m Los m vectores deben ser linealmente independientes Es una matriz no singular Tiene Matriz inversa |
| Ejercicios | Respuesta | ||||||||||||
Una empresa fabrica y vende dos tipos de bombas hidráulicas (1) normales (2) extra grandes. El proceso de manufactura asociado en la fabricación de las bombas: ensamblado, pintura y prueba. La contribución a las utilidades por la venta de una bomba normal de $50 y la utilidad de una bomba extra grande $75. Existen disponibles por semana 4800 horas de tiempo de ensamble, 1980 de tiempo de pintura y 900hrs de tiempo de prueba.se espera vender menos de 300 bombas normales y a lo más 180 de las extra grandes por semana.
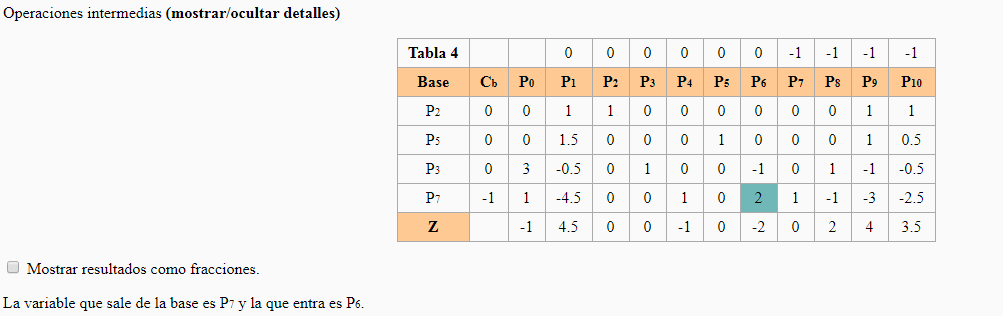
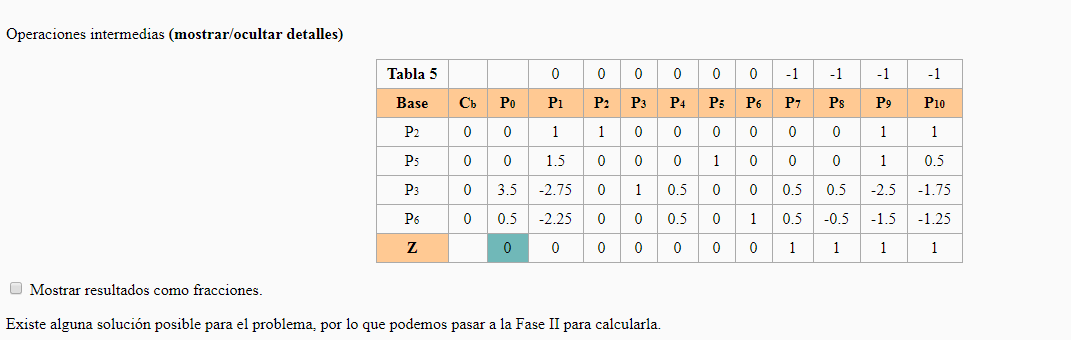
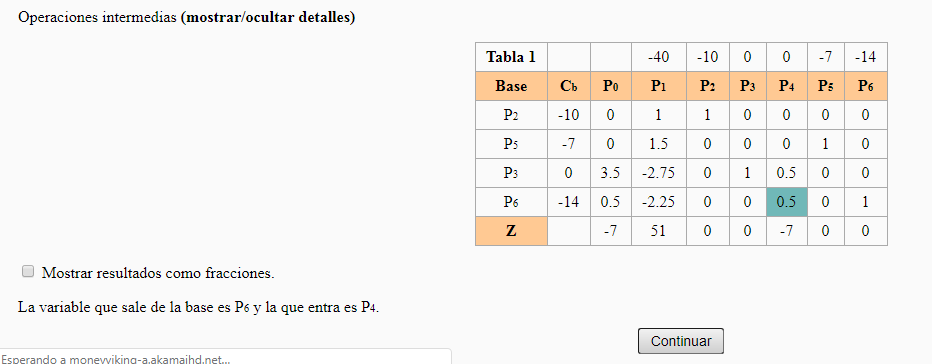
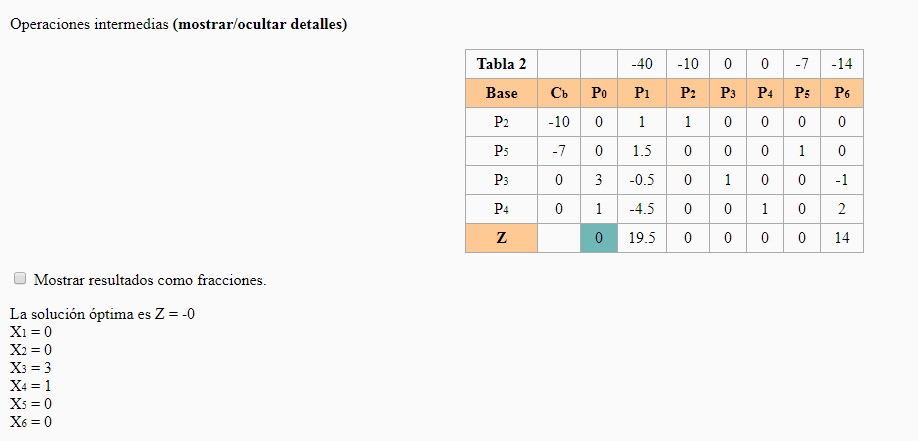
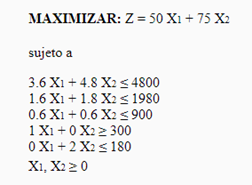 Modelo ampliado Modelo ampliado | Método Simplex de las Dos Fases Fase I 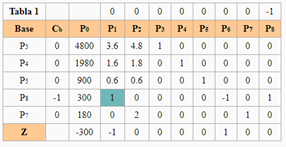 La variable que sale de la base es P8 y la que entra es P1. La variable que sale de la base es P8 y la que entra es P1.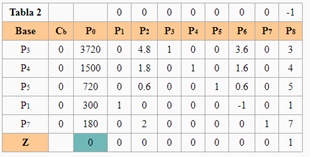 Existe alguna solución posible para el problema, por lo que podemos pasar a la Fase II para calcularla. Existe alguna solución posible para el problema, por lo que podemos pasar a la Fase II para calcularla.Fase II 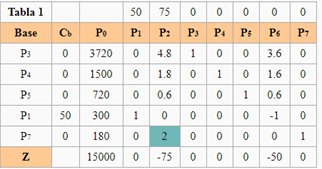 La variable que sale de la base es P7 y la que entra es P2. La variable que sale de la base es P7 y la que entra es P2.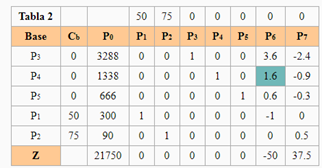 La variable que sale de la base es P4 y la que entra es P6 La variable que sale de la base es P4 y la que entra es P6 | ||||||||||||
| En limpieza SA se usan las materias primas I y II para producir dos soluciones limpiadoras domésticas, A y B. La disponibilidad diaria de las materias primas I y II es de 150 y 145 unidades, respectivamente. Una unidad de solución A consume 0.5 unidades de materia prima I y 0.6 unidad de materia prima II, una unidad de solución B requiere 0.5 unidad de materia prima I y 0.4 unidad de materia prima II. Las utilidades unitarias de las soluciones A y B son de $8 y $10 respectivamente, La demanda diaria de la solución A está entre 30 y 150 unidades y la de la solución B entre 40 y 200 unidades. Cuánto debe producir de A y B. PLANTEAMIENTO DEL PROBLEMA Modelo Ampliado 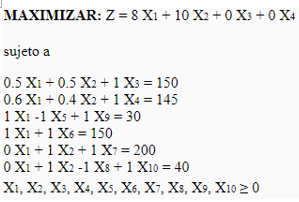 | RESOLVIENDO POR EL MÉTODO GRÁFICO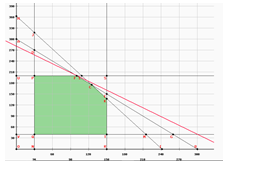 RESOLVIENDO CON EL MÉTODO DE LAS DOS FASES RESOLVIENDO CON EL MÉTODO DE LAS DOS FASESForma Estándar FASE 1. 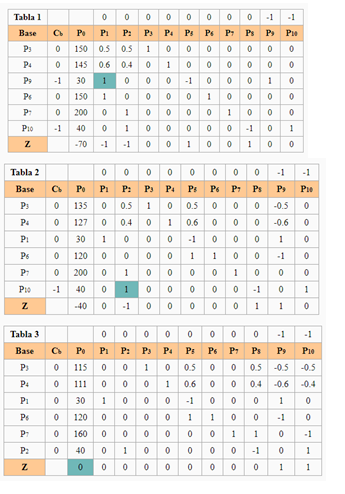 Al existir una posible solución pasamos a la FASE 2. Al existir una posible solución pasamos a la FASE 2.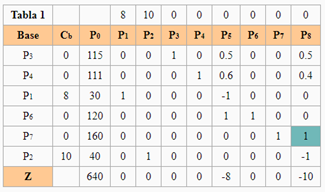 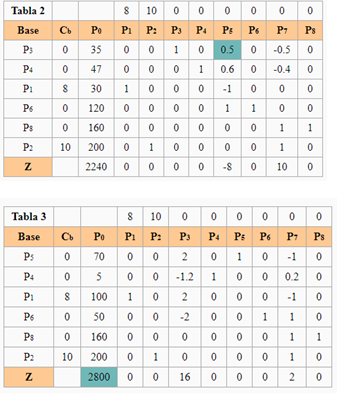 La solución Óptima es : La solución Óptima es :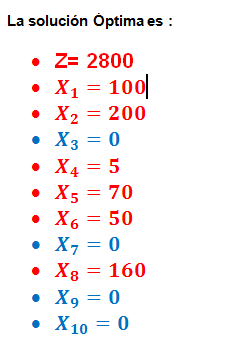 |
Ludwig von Bertalanffy

Biólogo alemán, nació el 19 de septiembre de 1901 en Viena, Austria.
Estudió historia del arte, filosofía y biología en la Universidad de Innsbruck y de Viena y, en ésta última finalizó el doctorado en 1926 leyendo su tesis doctoral sobre la psicofísica y Gustav Fechner.
En 1928 propuso una teoría general sobre los sistemas como una herramienta amplia que podría ser compartida por muchas ciencias distintas.
Esta teoría contribuyó a la aparición de nuevo paradigma científico basado en la interrelación entre los elementos que forman los sistemas. Previamente se consideraba que los sistemas en su conjunto eran iguales a la suma de sus partes, y que podían ser estudiados a partir del análisis individual de sus componentes; Bertalanffy puso en duda tales creencias.
Desde que fue creada, la teoría general de sistemas ha sido aplicada a la biología, a la psicología, a las matemáticas, a las ciencias computacionales, a la economía, a la sociología, a la política y a otras ciencias exactas y sociales, especialmente en el marco del análisis de las interacciones.
En 1939 trabajó como profesor en la Universidad de Viena, en la que estuvo hasta 1948. En 1949 emigró a Canadá y así siguió sus investigaciones en la Universidad de Ottawa hasta 1954. Después se traslada a Los Ángeles para trabajar en el Mount Sinai Hospital desde 1955 hasta 1958.Impartió clases de biología teórica en la canadiense Universidad de Alberta en Edmonton de 1961 a 1969. Su último trabajo fue como profesor en el Centro de biología Teórica de la Universidad Estatal de Nueva York en Búfalo, de 1969 a 1972.
Murió el 12 de junio de 1972.
Cibergrafía:
Figueroba, A. (s.f.). Psicología y mente. Recuperado el 9 de Agosto de 2018, de Psicología y mente: https://psicologiaymente.com/psicologia/teoria-general-de-sistemas-ludwig-von-bertalanffy
Ruiz, L. P. (2010 de Mayo de 3). Teoria General de Sistema (T.G.S). Recuperado el 9 de Agosto de 2018, de Teoria General de Sistema (T.G.S): http://teoriageneraldesistemaipsm.blogspot.com/2010/05/biografia-de-ludwig-von-bertalanffy.html
Imagen
Desconocido.[2007]BERTALANFFY[imagen]recuperado de:http://www.systemique.org/Idres/Media/bertalanffy.gif
Estudió historia del arte, filosofía y biología en la Universidad de Innsbruck y de Viena y, en ésta última finalizó el doctorado en 1926 leyendo su tesis doctoral sobre la psicofísica y Gustav Fechner.
En 1928 propuso una teoría general sobre los sistemas como una herramienta amplia que podría ser compartida por muchas ciencias distintas.
Esta teoría contribuyó a la aparición de nuevo paradigma científico basado en la interrelación entre los elementos que forman los sistemas. Previamente se consideraba que los sistemas en su conjunto eran iguales a la suma de sus partes, y que podían ser estudiados a partir del análisis individual de sus componentes; Bertalanffy puso en duda tales creencias.
Desde que fue creada, la teoría general de sistemas ha sido aplicada a la biología, a la psicología, a las matemáticas, a las ciencias computacionales, a la economía, a la sociología, a la política y a otras ciencias exactas y sociales, especialmente en el marco del análisis de las interacciones.
En 1939 trabajó como profesor en la Universidad de Viena, en la que estuvo hasta 1948. En 1949 emigró a Canadá y así siguió sus investigaciones en la Universidad de Ottawa hasta 1954. Después se traslada a Los Ángeles para trabajar en el Mount Sinai Hospital desde 1955 hasta 1958.Impartió clases de biología teórica en la canadiense Universidad de Alberta en Edmonton de 1961 a 1969. Su último trabajo fue como profesor en el Centro de biología Teórica de la Universidad Estatal de Nueva York en Búfalo, de 1969 a 1972.
Murió el 12 de junio de 1972.
Cibergrafía:
Figueroba, A. (s.f.). Psicología y mente. Recuperado el 9 de Agosto de 2018, de Psicología y mente: https://psicologiaymente.com/psicologia/teoria-general-de-sistemas-ludwig-von-bertalanffy
Ruiz, L. P. (2010 de Mayo de 3). Teoria General de Sistema (T.G.S). Recuperado el 9 de Agosto de 2018, de Teoria General de Sistema (T.G.S): http://teoriageneraldesistemaipsm.blogspot.com/2010/05/biografia-de-ludwig-von-bertalanffy.html
Imagen
Desconocido.[2007]BERTALANFFY[imagen]recuperado de:http://www.systemique.org/Idres/Media/bertalanffy.gif
C. W Churchman

Churchman nació en Filadelfia, Pensilvania el 29 de agosto de 1913.
Estudió filosofía en la Universidad de Pensilvania. Obtuvo una licenciatura en 1935, una maestría en 1936 y un doctorado en filosofía en 1938, su tesis de doctorado se llamó “Hacia una lógica general de las proposiciones”.
Antes de terminar su tesis doctoral, en 1937, se convirtió en instructor de Filosofía, también en la Universidad de Pennsylvania. Al finalizar sus estudios, fue nombrado profesor asistente en la Universidad.
Durante la Segunda Guerra Mundial se dirigió la sección de matemáticas del Laboratorio de Artillería EE.UU. en el Arsenal de Frankford en Filadelfia e ideó una forma de probar munición para armas pequeñas y detonadores basado en los métodos estadísticos de bioensayo. También se investigó la teoría de la detonación , aplicando fotografía de alta velocidad.
En 1945, en Pennsylvania, fue elegido Presidente del Departamento de Filosofía. En 1951 se trasladó a la Case Institute of Technology en Cleveland, Ohio , y hasta 1957 fue profesor de Administración de Ingeniería de la Case. En 1957, se unió a la facultad de la Universidad de California en Berkeley y se quedó allí como profesor emérito tras su jubilación.
Entre sus trabajos más destacados se encuentran “Teoría de Interferencia Experimental” en 1948, y “Métodos de Investigación” con Ackoff en 1950. Churchman y Ackoff se juntaron el departamento de administración de ingeniería en el Case Institute of Technology donde llevaron a cabo una investigación y organizaron algunos de los primeros programas de posgrado en el campo de investigación de operaciones.
Aún en Case junto con Ackoff , publicaron el primer libro de texto de “Introducción a la Investigación de Operaciones”, en 1957 y asumió la editorial de la revista “Ciencia de la Administración”, donde se mantuvo hasta1960.
Las fases del método de la Investigación de Operaciones establecidas como interactuantes por Churchman y Ackoff son:
– Formulación del problema.
– Construcción de un modelo.
– Obtención de una solución.
– Prueba del modelo y la solución.
– Implantación y control de la solución.
Churchman fue conocido internacionalmente por ser el pionero en investigación de operaciones, análisis de sistemas y éticas. Murió el 21 de marzo del 2004.
Referencias
Tareas Universitarias. (22 de Octubre de 2012). Recuperado el 25 de Agosto de 2018, de Tareas Universitarias: https://tareasuniversitarias.com/c-west-churchman.html
Desconocido.[2012]Churchman.[imagen]recuperado de: http://4.bp.blogspot.com/-OzOMVkdwe_4/T0EzPREpndI/AAAAAAAAACs/34a4jqM2zKI/s1600/churchman_1.jpg
Estudió filosofía en la Universidad de Pensilvania. Obtuvo una licenciatura en 1935, una maestría en 1936 y un doctorado en filosofía en 1938, su tesis de doctorado se llamó “Hacia una lógica general de las proposiciones”.
Antes de terminar su tesis doctoral, en 1937, se convirtió en instructor de Filosofía, también en la Universidad de Pennsylvania. Al finalizar sus estudios, fue nombrado profesor asistente en la Universidad.
Durante la Segunda Guerra Mundial se dirigió la sección de matemáticas del Laboratorio de Artillería EE.UU. en el Arsenal de Frankford en Filadelfia e ideó una forma de probar munición para armas pequeñas y detonadores basado en los métodos estadísticos de bioensayo. También se investigó la teoría de la detonación , aplicando fotografía de alta velocidad.
En 1945, en Pennsylvania, fue elegido Presidente del Departamento de Filosofía. En 1951 se trasladó a la Case Institute of Technology en Cleveland, Ohio , y hasta 1957 fue profesor de Administración de Ingeniería de la Case. En 1957, se unió a la facultad de la Universidad de California en Berkeley y se quedó allí como profesor emérito tras su jubilación.
Entre sus trabajos más destacados se encuentran “Teoría de Interferencia Experimental” en 1948, y “Métodos de Investigación” con Ackoff en 1950. Churchman y Ackoff se juntaron el departamento de administración de ingeniería en el Case Institute of Technology donde llevaron a cabo una investigación y organizaron algunos de los primeros programas de posgrado en el campo de investigación de operaciones.
Aún en Case junto con Ackoff , publicaron el primer libro de texto de “Introducción a la Investigación de Operaciones”, en 1957 y asumió la editorial de la revista “Ciencia de la Administración”, donde se mantuvo hasta1960.
Las fases del método de la Investigación de Operaciones establecidas como interactuantes por Churchman y Ackoff son:
– Formulación del problema.
– Construcción de un modelo.
– Obtención de una solución.
– Prueba del modelo y la solución.
– Implantación y control de la solución.
Churchman fue conocido internacionalmente por ser el pionero en investigación de operaciones, análisis de sistemas y éticas. Murió el 21 de marzo del 2004.
Referencias
Tareas Universitarias. (22 de Octubre de 2012). Recuperado el 25 de Agosto de 2018, de Tareas Universitarias: https://tareasuniversitarias.com/c-west-churchman.html
Desconocido.[2012]Churchman.[imagen]recuperado de: http://4.bp.blogspot.com/-OzOMVkdwe_4/T0EzPREpndI/AAAAAAAAACs/34a4jqM2zKI/s1600/churchman_1.jpg
R.L. Ackoff

Nació en Filadelfia en 1919.
Estudió arquitectura y filosofía de la ciencia en la Universidad de Pennsylvania en Filadelfia, donde se doctoró en 1947. Su vida académica comenzó en la Wayne University de Detroit, siguió en el Case Institute of Technology y, más tarde, en la Universidad de Pennsylvania, donde desarrolló la mayor parte de su carrera hasta 1986, año de su jubilación y de su paso a la condición de profesor emérito.
Fue catedrático y director del Departamento de Ciencia de los Sistemas Sociales en la Wharton School de la Universidad de Pennsylvania.
Profesor visitante de la Olin School of Business, de la Universidad de Washington en San Luis, de la de Birmingham, Nacional Autónoma de México (UNAM) y Lisboa.
Ha sido presidente de la Operations Research Society of America, fundador y vicepresidente del Institute of Management Sciences, ex presidente de la Society of Gerencial Systems Reserach, miembro de la Academia de Ciencias Naturales de Rusia. Presidente de Interact, Institute for Interactive Managemenet.
Entre sus libros:
Referencias
Infoamérica. (2013). Recuperado el 2018 de agosto de 25, de Infoamérica: https://www.infoamerica.org/teoria/ackoff1.htm
Desconocido.[2013].ackoff[imagen]recuprado de:https://www.infoamerica.org/teoria/ackoff1.htm
Estudió arquitectura y filosofía de la ciencia en la Universidad de Pennsylvania en Filadelfia, donde se doctoró en 1947. Su vida académica comenzó en la Wayne University de Detroit, siguió en el Case Institute of Technology y, más tarde, en la Universidad de Pennsylvania, donde desarrolló la mayor parte de su carrera hasta 1986, año de su jubilación y de su paso a la condición de profesor emérito.
Fue catedrático y director del Departamento de Ciencia de los Sistemas Sociales en la Wharton School de la Universidad de Pennsylvania.
Profesor visitante de la Olin School of Business, de la Universidad de Washington en San Luis, de la de Birmingham, Nacional Autónoma de México (UNAM) y Lisboa.
Ha sido presidente de la Operations Research Society of America, fundador y vicepresidente del Institute of Management Sciences, ex presidente de la Society of Gerencial Systems Reserach, miembro de la Academia de Ciencias Naturales de Rusia. Presidente de Interact, Institute for Interactive Managemenet.
Entre sus libros:
- Progress in Operations Reseach, I. Wiley, Nueva York, 1961
- Scientific Method, Wiley, Nueva York, 1962;
- On Purposeful Systems (con F. E. Emery), Aldine-Atherton, Chicago, 1972;
- Redesigning the Future, John Wiley & Sons, Nueva York, 1974;
- The Democratic Corporation: A Radical Prescription for Recreating Corporate America and Rediscovering Success, Oxford University Press, Nueva York, 1994;
- Re-Creating the Corporation: A Design of Organizations for the 21st Century, Oxford University Press, Nueva York, 1999.
Infoamérica. (2013). Recuperado el 2018 de agosto de 25, de Infoamérica: https://www.infoamerica.org/teoria/ackoff1.htm
Desconocido.[2013].ackoff[imagen]recuprado de:https://www.infoamerica.org/teoria/ackoff1.htm
R. Bellman

Nació en Brooklyn, Nueva York 26 de agosto de 1920
Fue un matemático aplicado, cuya mayor contribución fue la metodología denominada programación dinámica.
Bellman estudió matemáticas en la Universidad de Brooklyn, donde obtuvo el pregrado, y luego la maestría en la Universidad de Wisconsin. Posteriormente comenzó a trabajar en el Laboratorio Nacional Los Álamos en el campo de la física teórica. En 1946 obtuvo su doctorado en la Universidad de Princeton.
Los intereses de Richard Bellman comenzaron a enfatizar la biología y la medicina, que se identificó como “las fronteras de la ciencia contemporánea. En 1967, se convirtió en editor fundador de la revista Mathematical Biosciences que se especializó en la publicación de la investigación matemática aplicada de temas médicos y biológicos. En 1985, el Premio Bellman en Matemáticas Biosciences fue creado en su honor, siendo premio cada dos años a mejor trabajo de investigación de la revista.
También ejerció la docencia en la universidad del sur de California(EE. UU.), fue socio de la Academia Americana de las Artes y las Ciencias (1975) y de la Academia Nacional Americana de Ingeniería (1977). En 1979 el IEEE le otorgó la medalla de honor por su contribución a la teoría de los sistemas de control y de los procesos de decisión, en especial por su contribución con la programación dinámica y por la ecuación de Bellman.
Murió en Los Angeles California 19 de marzo de 1984
Referencias
Desconocido. (2005). Biographies. 09/09/2018, de Richard Ernest Bellman Sitio web: http://www-history.mcs.st-andrews.ac.uk/Biographies/Bellman.html
Desconocido.(2012)Bellman[imagen] recuperado de: https://upload.wikimedia.org/wikipedia/en/thumb/7/7a/Richard_Ernest_Bellman.jpg/220px-Richard_Ernest_Bellman.jpg
Fue un matemático aplicado, cuya mayor contribución fue la metodología denominada programación dinámica.
Bellman estudió matemáticas en la Universidad de Brooklyn, donde obtuvo el pregrado, y luego la maestría en la Universidad de Wisconsin. Posteriormente comenzó a trabajar en el Laboratorio Nacional Los Álamos en el campo de la física teórica. En 1946 obtuvo su doctorado en la Universidad de Princeton.
Los intereses de Richard Bellman comenzaron a enfatizar la biología y la medicina, que se identificó como “las fronteras de la ciencia contemporánea. En 1967, se convirtió en editor fundador de la revista Mathematical Biosciences que se especializó en la publicación de la investigación matemática aplicada de temas médicos y biológicos. En 1985, el Premio Bellman en Matemáticas Biosciences fue creado en su honor, siendo premio cada dos años a mejor trabajo de investigación de la revista.
También ejerció la docencia en la universidad del sur de California(EE. UU.), fue socio de la Academia Americana de las Artes y las Ciencias (1975) y de la Academia Nacional Americana de Ingeniería (1977). En 1979 el IEEE le otorgó la medalla de honor por su contribución a la teoría de los sistemas de control y de los procesos de decisión, en especial por su contribución con la programación dinámica y por la ecuación de Bellman.
Murió en Los Angeles California 19 de marzo de 1984
Referencias
Desconocido. (2005). Biographies. 09/09/2018, de Richard Ernest Bellman Sitio web: http://www-history.mcs.st-andrews.ac.uk/Biographies/Bellman.html
Desconocido.(2012)Bellman[imagen] recuperado de: https://upload.wikimedia.org/wikipedia/en/thumb/7/7a/Richard_Ernest_Bellman.jpg/220px-Richard_Ernest_Bellman.jpg
George Bernard Dantzig

Nacido el 8 de noviembre de 1914 fue profesor, físico y matemático estadounidense, conocido por desarrollar el método simplex y es considerado como “El padre de la programación lineal”.
Debido a la fuerza aérea realizó sus grandes hazañas matemáticas, ya que necesitaba calcular el tiempo de duración de las etapas de un programa de despliegue, de un modo más óptimo y eficaz.
Estableció el problema general de Programación Lineal. Sin embargo los problemas planteados eran demasiado complejos para las computadoras más veloces de la época. Se hacía necesario desarrollar un método capaz de encontrar soluciones en un tiempo razonable.
En 1947 propuso el Método Simplex para resolver un problema de programación lineal.
Dio lugar a una nueva rama en la Programación Lineal en el año 1955, llamada Programación Estocástica o Programación Bajo Incertidumbre, desarrollada en su libro «Linear Programming under Uncertainty».
Las investigaciones de George Dantzig también incluyen aplicaciones de variables discretas, problema de la mochila, red y rutas de camino más corto, el método Simplex revisado, y mucho más. Un ejemplo de ello es otro método ampliamente utilizado hoy en día: el principio de descomposición, que desarrolló junto a Philip Wolfe, entre 1959 y 1960. Conocido como el método de Descomposición de Dantzig-Wolfe, establece pautas para encontrar la solución de problemas de gran tamaño, es decir, que implican grandes cantidades de datos y variables.
Fundó el Centro de Investigación Operativa (Operations Research Center).
Falleció el 13 de mayo de 2005
Referencias:
Desconocido. (2010). Biografiía George Bernard Dantzig. 09/09/2018, de PHP Simplex Sitio web: http://www.phpsimplex.com/biografia_Dantzig.htm
Desconocido.(2010)Gerge_Dantzig[imagen] recuperado de: http://www.phpsimplex.com/img/dantzig_iiasa.jpg
Debido a la fuerza aérea realizó sus grandes hazañas matemáticas, ya que necesitaba calcular el tiempo de duración de las etapas de un programa de despliegue, de un modo más óptimo y eficaz.
Estableció el problema general de Programación Lineal. Sin embargo los problemas planteados eran demasiado complejos para las computadoras más veloces de la época. Se hacía necesario desarrollar un método capaz de encontrar soluciones en un tiempo razonable.
En 1947 propuso el Método Simplex para resolver un problema de programación lineal.
Dio lugar a una nueva rama en la Programación Lineal en el año 1955, llamada Programación Estocástica o Programación Bajo Incertidumbre, desarrollada en su libro «Linear Programming under Uncertainty».
Las investigaciones de George Dantzig también incluyen aplicaciones de variables discretas, problema de la mochila, red y rutas de camino más corto, el método Simplex revisado, y mucho más. Un ejemplo de ello es otro método ampliamente utilizado hoy en día: el principio de descomposición, que desarrolló junto a Philip Wolfe, entre 1959 y 1960. Conocido como el método de Descomposición de Dantzig-Wolfe, establece pautas para encontrar la solución de problemas de gran tamaño, es decir, que implican grandes cantidades de datos y variables.
Fundó el Centro de Investigación Operativa (Operations Research Center).
Falleció el 13 de mayo de 2005
Referencias:
Desconocido. (2010). Biografiía George Bernard Dantzig. 09/09/2018, de PHP Simplex Sitio web: http://www.phpsimplex.com/biografia_Dantzig.htm
Desconocido.(2010)Gerge_Dantzig[imagen] recuperado de: http://www.phpsimplex.com/img/dantzig_iiasa.jpg
Conceptos del mapa
| Concepto | Ideas básicas |
| Cambio |
|
| Homeóstasis |
|
| Era de la máquina |
|
| Renacimiento |
|
| Curiosidad |
|
| Análisis |
|
| Reduccionismo |
|
| Determinismo |
|
| Mecanicismo |
|
| Revolución Industrial |
|
| Trabajo |
|
| Máquina |
|
| Era de sistemas |
|
| Investigación de operaciones |
|
| Sistema |
|
| Pensamiento sistémico |
|
| Síntesis |
|
| Revolución Postindustrial |
|
| Sistemas deterministas |
|
| Sistemas Animados |
|
| Sistemas Sociales | Corporaciones Universidades Sociedades |
| Sistemas ecológicos | Contienen sistemas mecanicistas, sistemas organicistas y sistemas sociales que interactúan entre si Cumplen los propósitos de los organismos y sistemas sociales que constituyen sus partes |
| Fines | Son las metas Objetivos Ideales |
| Crecimiento | Aumentar en tamaño o numero |
| Desarrollo | Es aumentar la habilidad y el deseo de uno mismo para satisfacer las necesidades y los deseos legítimos tanto propios como los de los demás Incremento de la capacidad y la competencia Cuestión de aprendizaje |
Mapa:
https://www.goconqr.com/es-ES/p/15242211-SISTEMA-mind_maps
Referencias:
Ackoff.R(2002)Paradigma de Acoff.México
Desconocido,(2018).maquinas[imagen]recuperado de: http://caymansseo.com/wp-content/uploads/2018/01/maquinas.jpg
Desconocido.(2010)sociedad[imagen] recuperado de: https://www.emprendepyme.net/wp-content/uploads/2017/05/sociedades-profesionales.jpg
Deconocido.(2012)rev.industrial[imagen] recuperado de: https://mihistoriauniversal.com/wp-content/uploads/revolucion_industrial_locomotora-660x330.jpg
Desconocido.(2010)servivo[imagen]recuperado de: http://2.bp.blogspot.com/-tJ83wLp_H1Y/Usa4GmpBAKI/AAAAAAAAAUo/D7Km0H-M4BE/s1600/SERES+VIVOS.png
Desconocido.(2013)operaciones[imagen]recuperado de: https://s3a2.files.wordpress.com/2013/02/investigaciondeoperaciones.jpg?w=342&h=257
Desconocido(2018)renacimiento[imagen]recuperado de: https://fthmb.tqn.com/hhBCWzewXnm40cGNs0ktNbW0PaA=/768x0/filters:no_upscale():max_bytes(150000):strip_icc():format(webp)/Uomo_Vitruviano-56a5ab663df78cf772895707.jpg
Desconocido (2018)cambio[imagen]recuperado de: http://cio.com.mx/wp-content/uploads/2017/05/administracion-del-cambio.jpg
clasificación de los sistemas
| Tipos de Sistemas | Definición | Ejemplo | Página |
| Abstracto | Compuesto por elementos que no pueden ser tocados o sentidos directamente, es decir cosas intangibles | Software | Anónimo.TGS01.Recuperdo el 12 de agosto de 2018 de TGS01:https://sites.google.com/site/ttggss001/tipos-de-sistemas/constitución/sistema-abstracto |
| Concreto | Está compuesto por elementos tangibles, perceptibles y las relaciones entre estos dentro del sistema y con el entorno | Computadora | Anónimo.TGS01.Recuperdo el 12 de agosto de 2018 de TGS01:https://sites.google.com/site/ttggss001/tipos-de-sistemas/constitución/sistema-concreto |
| Abierto | Tiene entradas y salidas de información y los procesos, tiene intercambio con el medio. Sus limitaciones están ubicadas en la aptitud de sus procesos para trabajar sus entradas de manera que no pierda energía | Cuerpo humano | Anonimo.TGS01.Recuperdo el 12 de agosto de 2018 de TGS01:https://sites.google.com/site/ttggss001/tipos-de-sistemas/naturaleza/sistema-abierto |
| Cerrado | Es aquel que no tiene intercambio con otro medio emitiendo su propia energía | Prueba al vacío | Anonimo.TGS01.Recuperdo el 12 de agosto de 2018 de TGS01:https://sites.google.com/site/ttggss001/tipos-de-sistemas/naturaleza/sistema-cerrado |
| Estático | Cuando las relaciones que se establecen entre las variables son contemporáneas o permanecen en el tiempo | Calculadora | (20011,11)Sistema estático.ClubEnsayos.com recuperado el 12 de agosto de 2018 de https://club.ensayos.com/Acontecimientos sociales/sistema-estatico/107147.html |
| Dinámico | Son modelos matemáticos de sistemas que varían a lo largo del tiempo que establecen como será en el futuro | Sociedad | Anónimo, Mathworks. recuperado el 12 de agosto de 2018 de Math Works: https://es.mathworks.com/discovery/sistemas-dinamico.html |
| Homeostático | Conjunto de estructuras capaces de compensar un cambio en las condiciones internas para mantenerse en una condición estable y constante | Temperatura | De Paola,Macarena(2012,11,13).Prezi, recuperado el 12 de agosto de 2018 de https://Prezi.com/m/whhq_/703jlfp/sistemas-homeostaticos/ |
Tarea IV
Participación 8C

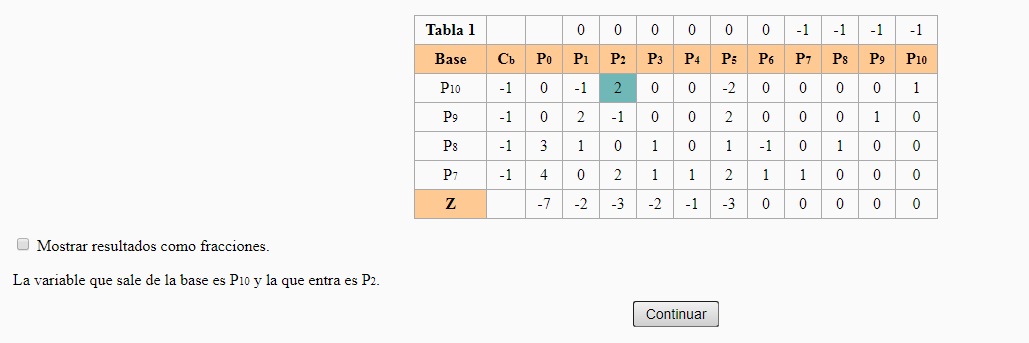
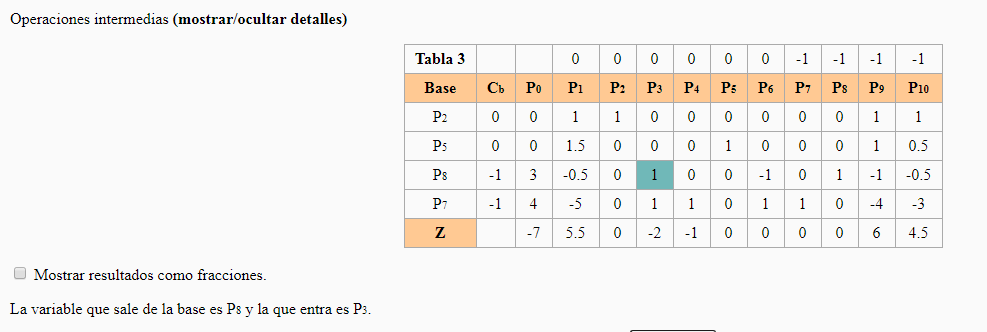
Participación 1f
Primal
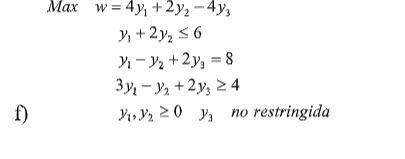
Dual
Min g = 6x1 +8x2+4x3
s.a.
x1+x2+3x3 >=4
2x1-x2-x3> = 2
2x2+2x3 = -4
x1> = 0
x2 no restringida
x3< = 0
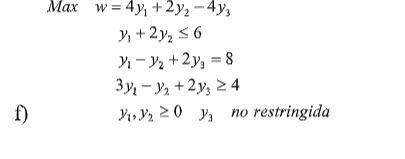
Dual
Min g = 6x1 +8x2+4x3
s.a.
x1+x2+3x3 >=4
2x1-x2-x3> = 2
2x2+2x3 = -4
x1> = 0
x2 no restringida
x3< = 0
Participación 2b
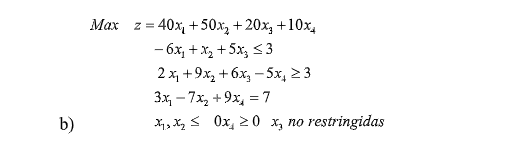
Min g= 3y1+3y2+7y3
s. a.
-6y1+2y2+3y3<= 40
y1+9y2-7y3< = 50
5y1+6y2=20
-5y2+9y3>= 10
y1>=0
y2<=0
y3 no restringida
TAREA V
Podcast
Conociendo a los alumnos
Póngase en contacto con el escritor
- Naucalpan, Estado de Mexico, Mexico